Sistem Bilangan Biner, Desimal, dan Heksadesimal

Sistem Bilangan - Di dalam keseharian kita mengenal nominal bilangan seribu, puluhan ribu, ratusan ribu dan bahkan jutaan yang di pakai sebagai format hitungan mata uang resmi Negara kita, yaitu Indonesia. Nah nominal-nominal bilangan yang saya sebutkan tadi merupakan bilangan berbasis 10 (Desimal atau radiks 10).

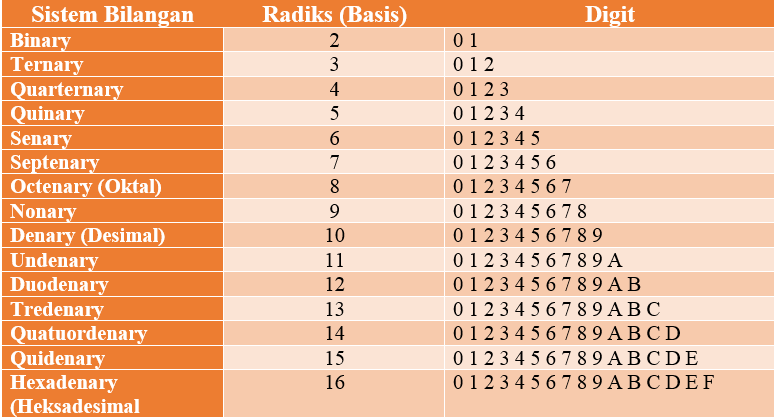
Lihat tabel diatas terdapat banyak jenis sistem bilangan saat ini, diantaranya bilangan berbasis 2 (Biner), berbasis 3 (Ternary), berbasis 4 (Quarternary), berbasis 10 (Denary) hingga bilangan berbasis 16 (Hexadenary). Namun diantara banyaknya jenis sistem bilangan yang saya sebutkan diatas, hanya sistem bilangan Biner, Oktal, Desimal dan Heksadesimal yang sering digunakan dalam pengoprasian komputer.

Dalam pembahasan saat ini setidaknya ada sembilan point subpokok bahasan yang akan kita pelajari pada materi sistem bilangan ini, diantaranya:

Daftar Isi

• Pengertian Sistem Bilangan
• Format bilangan
• Pengertian Bilangan Biner
• Konversi Bilangan Biner Ke Desimal
• PengertianBilangan Oktal
• Konversi Bilangan Oktal ke Desimal
• Pengertian Bilangan Desimal
• Pengertian Bilangan Heksadesimal
• Konversi Bilangan Heksadesimal Ke Desimal
• Uji Pemahaman

Pengertian Sistem Bilangan

Sistem bilangan adalah simbol-simbol yang merepresentasikan bilangan sebagai cara untuk mewakili ukuran besaran dari suatu benda fisik.

Format Bilangan

Dalam Penulisan bilangan harus menggunakan konvensi notasi, Kenapa? supaya dapat membedakan format dari sebuah bilangan dengan bilangan lainnya, bagaimana paham maksudnya?

Jadi begini contohnya, untuk penulisan bilangan 220 basis 2 (Biner) di tulis menjadi 220₂ Sedangkan penulisan bilangan 310 basis 10 (Desimal) di tulis 310₁₀  begitu juga seterusnya untuk bilangan Oktal dan Heksadesimal. Gimana, Pasti paham kan?

Pengertian Bilangan Biner

Bilangan Biner (Binary) adalah bilangan yang hanya mengenal dua buah angka numerik yakni 0 dan 1, Nilai 0 mencerminkan keadaan arus listrik HIGH, sedangkan nilai 1 mencerminkan tidak adanya arus listrik atau LOW.

Konversi Bilangan Biner ke Desimal

Setelah mengetahui apa itu bilangan Biner, sekarang saatnya untuk praktik bagaimana cara mengkonversi bilangan Biner ke Desimal. Rumusnya sebagai berikut:

∑(A × 2^b)

Keterangan Rumus diatas:

• A = Bernilai 0 atau 1
• b  = bernilai .... -4, -3, -2, -1, 0, 1, 2, 3, 4,  (nilai negatif di implementasikan bilangan biner dengan angka di belakang koma)

1. Contoh soal dan penyelasaian konversi bilangan biner ke desimal tanpa angka dibelakang koma

1010₂ = (1 x 2³) + (0 x 2²) + (1 x 2¹) + (0 x 2⁰)

           = 8 + 0 + 2 + 0

           = 10₁₀

Hasil konversi dari bilangan biner 1010 ke desmial adalah 10

2. Contoh soal dan penyelasaian konversi bilangan biner ke desimal dengan angka dibelakang koma

1,110₂ = (1 x 2⁰) + (1 x 2^-1) + (1 x 2^-2) + (0 x 2^-3)

           = 1 + (1 x 0,5) + (1 x 0,25) + (0 x 0.125)

           = 1,75₁₀

Hasil Konversi dari bilangan biner 1,110 ke desimal adalah 1,75

Catatan:

Terdapat perbedaan yang signifikan pada contoh soal no 2 di atas dengan contoh soal no 1, apa perbedaanya? perbedaannya terletak pada angka di belakang koma dan pangkat negatif. mungkin akan ada pertanyaan yang muncul dalam benak kalian, seperti :

• Pertanyaan : kenapa ko pangkatnya di mulai dari pangkat 0?
• Jawban : Ya, karena angka di belakang koma hanya satu sehingga urutan pangkatnya adalah 0, -1, -2, -3 (coba lihat kembali pada keterangan rumus yang sudah di bahas diatas). lain hal jika ada dua angka di belakang koma maka urutan pangkatnya adalah 1, 0, -1, -2. Demikian juga jika ada 3 angka di belakang koma maka urutan pangkatnya menjadi 2, 1, 0, -1.
• Pertanyaan : bagaimana cara perhitungan untuk perpangkatan negatif?
• Jawaban : untuk menghitung pangkat negatif kamu harus mengingat lagi materi pelajaran matematika kelas 9 tentang pangkat negatif, penjelasan singkat jika pada soal diatas terdapat 2^-2 sama dengan 1/4 dan hasil dari 1/4 adalah 0.25.

Pengertian Bilangan Oktal

Bilangan Oktal (Octenary) adalah bilangan yang hanya mengenal 8 buah angka numerik yakni 0, 1, 2 , 3, 4, 5, 6, dan 7. Dalam penulisan bilangan oktal ini format yang digunakan N₈ (N adalah bilangan oktal)

Konversi Bilangan Oktal ke Desimal

Cara konversi bilangan Oktal (Octenary) ke bilangan desimal menggunakan rumus berikut:

∑(A × 8^b)

Keterangan Rumus diatas:

• A = Bernilai 0, 1, 2, 3, 4, 5, 6, 7
• b  = bernilai .... -4, -3, -2, -1, 0, 1, 2, 3, 4,  (nilai negatif di implementasikan bilangan biner dengan angka di belakang koma)

1. Contoh soal dan penyelasaian konversi bilangan oktal ke desimal tanpa angka dibelakang koma

₃₂₃₈ = (3 x 8²) + (2 x 8¹) + (3 x 8⁰)

           = 192 + 16 + 3

           = 211₁₀

Hasil konversi dari bilangan oktal 323 ke desmial adalah 211

2. Contoh soal dan penyelasaian konversi bilangan oktal ke desimal dengan angka dibelakang koma

_31,238 = (3 x 8¹) + (1 x 8⁰) + (2 x 8^-1) + (3 x 8^-2)

           = 24 + (1 x 1) + (2 x 0,125) + (3 x 0,0156)

                     = 24 + 1 + 0,25 + 0,0468

           = 25,2968₁₀

Hasil konversi dari bilangan oktal 31,23 ke desmial adalah 25,2968

Pengertian Bilangan Desimal

Sistem bilangan Desimal (Denary) atau bilangan berbasis 10 adalah bilangan yang memiliki 10 buah jenis angka numerik, yakni 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Dalam penulisan bilangan desimal ini menggunakan format N₁₀ (N adalah bilangan desimal).

Pengertian Bilangan Heksadesimal

Sistem bilangan Heksadesimal (Hexadenary) atau bilangan berbasis 16 adalah bilangan yang memiliki 10 buah jenis angka numerik dan 6 karakter, yakni 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, dan F. Dalam penulisan bilangan desimal ini menggunakan format N₁₆ (N adalah bilangan Heksadesimal). karakter A₁₆ pada bilangan heksadesimal mewakili nilai 10 kemudian di ikuti dengan karakter B₁₆ = 11, C₁₆ = 12, D₁₆ = 13, E₁₆ = 14, dan  F₁₆ = 15.

Konversi Bilangan Heksadesimal ke Desimal

Cara konversi bilangan Heksadesimal (Hexadenary) ke bilangan desimal menggunakan rumus berikut:

∑(A × 16^b)

Keterangan Rumus diatas:

• A = Bernilai 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
• b  = bernilai .... -4, -3, -2, -1, 0, 1, 2, 3, 4,  (nilai negatif di implementasikan bilangan biner dengan angka di belakang koma)

1. Contoh soal dan penyelasaian konversi bilangan heksadesimal ke desimal tanpa angka dibelakang koma

_A1216 = (A x 16²) + (1 x 16¹) + (2 x 8⁰)

                     = (10 x 256) + (1 x 16) + (2 x 1) 

           = 2560 + 16 + 1

           = 2578₁₀

Hasil konversi dari bilangan oktal A12 ke desmial adalah 2578

2. Contoh soal dan penyelasaian konversi bilangan heksadesimal ke desimal dengan angka dibelakang koma

_A12,2116 = (A x 16²) + (1 x 16¹) + (2 x 16⁰) + (2 x 16^-1) + (1 x 16^-2)

                = (10 x 256) + (1 x 16) + (2 x 1) + (2 x 0,0625) + (1 x 0,00391)

                          = 2560 + 16 + 2 + 0,125 + 0,00391

                = 2578,12891₁₀

Hasil konversi dari bilangan oktal A12,21 ke desmial adalah 2578,12891

Uji Pemahan Sistem Bilangan dengan Studi Kasus

Alhamdulillah kita telah selesai mempelajari materi tentang Sistem Bilangan secara runut dari awal hingga akhir, semoga apa yang saya sampaikan kali ini memberikan manfaat serta menambah pengetahuan buat kamu. akhir kata saya punya challenge buat kamu, silahkan uji pemahaman kamu dengan mengerjakan pertanyaan singkat yang ada dibawah ini. good luck and see you again!

Bagikan Artikel ini